Seismic Principles
1. A 4-story hospital, with emergency room, will be built on a site with SDS=0.45g and SD1=0.15g. The initial plan for the hospital includes an out-of-plane offset irregularity.
What is the Seismic Design Category (SDC)?
(a) SDC C
(b) SDC D
(c) SDC E
(d) SDC F
Solution
Best answer: (b)
Explanation
The Seismic Design Category for a building depends on what it is used for (the Risk Category) and the potential for ground shaking at the site (SDS and SD1). The Seismic Design Category is not influenced by irregularities.
Step 1 - Determine the Risk Category
Table 1604.5 in the California Building Code (CBC) can be used to identify the Risk Category. The Risk Category depends on what the building is going to be used for. From Table 1604.5, the Risk Category for a hospital with an emergency room would be IV.
Step 2 - Identify the Seismic Design Category
The procedures and tables for determining the Seismic Design Category are found in Section 1613.3.5 of the CBC. Based on the SDS and SD1 values that were given, and Risk Category IV, the building will be in Seismic Design Category D.
The best answer is (b).
Did you get this problem wrong?
The book Seismic Principles is the ultimate resource to help you as you are preparing for and taking the real exam. There is an explanation of Seismic Design Categories and three fully-worked examples in Section 3.8 of Seismic Principles.
2. A 2-story apartment complex with wood shear walls is in Seismic Design Category E.
What are the minimum requirements for the sill plate anchors for the shear walls?
(a) 5/8 in. dia. anchor bolts with plate washers every 4 ft
(b) 5/8 in. dia. anchor bolts with cut washers every 4 ft
(c) 5/8 in. dia. anchor bolts with plate washers every 6 ft
(d) 1/2 in. dia. anchor bolts with cut washers every 6 ft
Solution
Best answer: (c)
Explanation
Minimum requirements for anchor bolts are found in Section 2308.3.1 of the California Building Code (CBC). The 5/8 in. diameter bolts are required because the Seismic Design Category is E. The plate washers are required because it is a shear wall in Seismic Design Category D or E. The 6 ft spacing is okay because the structure in not over two stories.
Did you get this question wrong?
The book Seismic Principles, is the ultimate resource to help you as you are preparing for and taking the real exam. There are great illustrations in Seismic Principles that show you the requirements, instead of just telling you. For example, pages 152 and 153 illustrate anchor bolt requirements to give you a better understanding of what the CBC is talking about.
3. Two buildings, with the same story heights but different number of stories, will be constructed next to each other. The displacements shown below are the expected displacements during the design earthquake (including inelastic displacements).
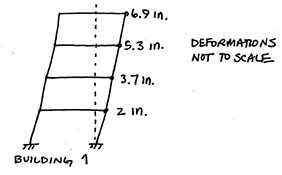
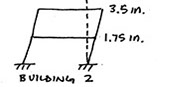
How far apart should the buildings be separated to avoid pounding?
(a) 3.8 in.
(b) 5.1 in.
(c) 7.2 in.
(d) 7.7 in.
Solution
Best answer: (b)
Explanation
Even though the sketches show both buildings deforming to the right, the expected displacements could occur either way. The critical location for the buildings to pound into each other would be at the roof elevation of the shorter building. Since it is unlikely that each building will experience its maximum deformation at the same point in a time, a square-root-sum-of-the-squares approach is used to calculate the appropriate spacing (see AISC 7-10 Section 12.12.3).
[(3.7 in.)^2 + (3.5 in.)^2]^0.5 = 5.1 in.
The best answer is (b).
Did you get this question wrong?
The book Seismic Principles, is the ultimate resource to help you as you are preparing for and taking the real exam. There are more than 200 examples in Seismic Principles that illustrate how to solve typical problems. Example 6.19 is a little harder than this problem because the inelastic displacement is not given and has to be calculated.
4. A 200 ft tall steel moment frame is being designed for a site with SD1=0.6g.
What is the maximum value for the period, T, that can be used when computing the seismic response coefficient, if a computer analysis indicates a period of 3.0 seconds?
(a) 1.7 sec
(b) 1.9 sec
(c) 2.7 sec
(d) 3.0 sec
Solution
Best answer: (c)
Explanation
ASCE 7 puts an upper limit on the period that can be used when computing the base shear force (the seismic response coefficient).
The four basic steps the check the upper limit are: 1) look up the parameters Ct and x, 2) compute Ta, 3) look up CU, and 4) compare CUTa with the period determined from the computer analysis.
Step 1 - Look up Ct and x
An empirical procedure for estimating the period of a building requires values for Ct and x. Values for these parameters can be looked up in Table 12.8-2 of ASCE 7-10.
Since the building has steel moment frames, Ct =0.028 and x=0.8.
Step 2 - Compute Ta
An approximate period, Ta, is calculated with the equation: Ta=Cthnx, where hn is the height of the building.
Ta = (0.028)*(200)^(0.8) = 1.94
Step 3 - Look up CU
The upper limit when using a period determined from a computer model is equal to CUTa.
For SD1=0.6g, CU will be 1.4
Step 4 - Compare CUTa with the period determined from the computer analysis
CUTa = (1.4)(1.94) = 2.7 sec.
Since the period determined from the computer analysis (given as 3.0 seconds) exceeds this limit, the limiting value of 2.7 seconds is the maximum value that can be used for the period when determining the seismic response coefficient (the base shear).
Choice (c) is the best answer.
Did you get this question wrong?
The book Seismic Principles, is the ultimate resource to help you as you are preparing for and taking the real exam. Versions of the ASCE 7 tables are provided in Seismic Principles, so that all the information you need for a problem (tables, equations, explanations, and examples) are all on one page. For example, look at Section 3.13 of Seismic Principles and see for yourself.
5. Which brace configurations can be used for an SCBF?
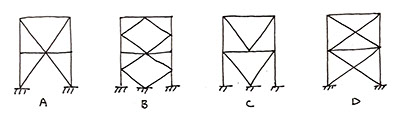
(a) A and D
(b) A, B, and D
(c) A, C, and D
(d) A, B, C, and D
Solution
Best answer: (c)
Explanation
SCBF stands for special concentrically braced frame. The requirements for special concentrically braced frames are found in the AISC Seismic Provisions (AISC 341, Chapter F). K-bracing configurations (similar to image B) are specifically prohibited for SCBFs. The other bracing configurations shown are allowed, although additional requirements apply to cases A and C.
Did you get this question wrong?
The California Building Code (CBC) requires most steel buildings to constructed in accordance with AISC 341, but it does not reprint all of the requirements. Most people do not have a current copy of AISC 341 and are not familiar with this document. The book Seismic Principles, provides a summary of the requirements for various steel systems, making questions like this one easy. Take a look at Section 10.3 from Seismic Principles.
6. The image below shows a one-story building with a flexible roof diaphragm. How much of the applied load is resisted by the frame on grid line A?
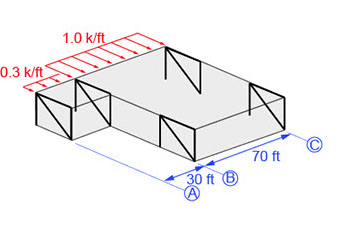
(a) 4.5 kips
(b) 15.8 kips
(c) 26.3 kips
(d) 35 kips
Solution
Best answer: (a)
Did you get this question wrong?
You are not alone. Very few engineering graduates have learned anything about diaphragm analysis. Unfortunately, several of the questions on the real exam will involve diaphragm analysis. The procedures for flexible and rigid diaphragm analysis are not covered in ASCE 7 or the CBC. You will need an additional reference in order to have the pertinent equations and examples for their use. Seismic Principles devotes an entire chapter to explaining flexible diaphragm analysis and has more than twenty-five fully-worked examples.
Explanation
Example 4.8 in Seismic Principles is identical the question above.
7. Which of the following is not exempt from seismic design requirements?
(a) Exterior window shades in SDC B
(b) A 1000 lb air handling unit on a roof in SDC B
(c) A 15 lb compressor unit on a roof in SDC D
(d) A 7 ft tall floor-supported cabinet in SDC C
Solution
Best answer: (d)
Explanation
This question is about non-structural components. The requirements for non-structural components are found in Chapter 13 of ASCE 7. Many non-structural components are exempt and do not need to be specifically designed to resist seismic forces.
Choices (a) and (b) are exempt, because the Seismic Design Category (SDC) is B, and all non-structural components are exempt in B except parapets supported by bearing or shear walls and tall bookshelves/cabinets.
Choice (c) is exempt, because all mechanical and electrical components that weigh less than 20 lbs are exempt.
Choice (d) is not exempt because it is a floor-supported cabinet that is over 6 ft tall. This non-structural component needs to be designed to withstand seismic forces without tipping over.
Did you get this question wrong?
Table 11.1 in Seismic Principles (including footnotes) explains which types of non-structural components are exempt.
8. A building roof has 150 kips of the equivalent lateral force acting at that level. The seismic weight of the roof is 475 kips. The importance factor for the building is 1.0 and the diaphragms are all flexible. SDS for the site is 1.7g.
What is the diaphragm design force for the roof?
(a) 150 kips
(b) 161 kips
(c) 247 kips
(d) 323 kips
Solution
Best answer: (b)
Explanation
The procedure for calculating diaphragm design forces is given in ASCE 7 Section 12.10.1. For this particular problem:
Fpx = (150 kips)*(475 kips)/(150 kips) = 150 kips
Fpx,min = 0.2*(1.7)*(1.0)*(475 kips) = 161 kips
Fpx,max = 0.4*(1.7)*(1.0)*(475 kips) = 322 kips
Since the minimum value is greater than the value given by the first equation, it will govern. The best answer is (b).
Did you get this question wrong?
The book Seismic Principles, is the ultimate resource to help you as you are preparing for and taking the real exam. The formulas for computing diaphragm design forces can be confusing. Section 4.8 of Seismic Principles presents the diaphragm formulas and demonstrates how they are used for both floor and roof diaphragms.
9. A cantilevered concrete wall is 25 ft wide, 20 ft tall, and 8 inches thick. The modulus of elasticity of the concrete is 3500 ksi and the shear modulus is 1500 ksi.
What is the stiffness of the concrete wall?
(a) 1,250 k/in
(b) 2,900 k/in
(c) 4,874 k/in
(d) 6,530 k/in
Solution
Best answer: (d)
Explanation
Stiffness formulas for common walls, frames, and columns are given in Figure 2.7 of Seismic Principles. For a cantilever wall, the stiffness is a function of:
A - the cross-sectional area of the wall
I - the moment of inertia of the wall
h - the height of the wall
E - the modulus of elasticity
G - the shear modulus of elasticity.
Step 1 - Get values for A, I, h, and G (being careful with units)
For the wall in question, the cross-sectional area is:
A = (8 in.)(25 ft * 12 in./ft) = 2400 in.^2.
For the wall in question, the moment of inertia is:
I = (8 in.)(25 ft * 12 in./ft)^3/12 = 18,000,000 in.^4
The height, modulus of elasticity, and shear modulus were given:
h = (20 ft * 12 in./ft) = 240 in.
E = 3500 ksi
G = 1500 ksi
Step 2 - Compute the stiffness
Using the formula from Figure 2.7 in Seismic Principles:
k = 1/{(240 in.)^3/(3*(3500 ksi)(18,000,000 in.^4)) +
1.2*(240 in.)/[(2400 in.^2)(1500 ksi)]} = 6530 k/in.
The stiffness of the wall is 6530 k/in. so (d) is the best answer.
Did you get this question wrong?
You cannot solve problems like this in a reasonable amount of time unless you have a reference with the basic stiffness formulas. The book Seismic Principles, is the ultimate resource to help you as you are preparing for and taking the real exam. Figure 2.7 has stiffness formulas for basic structural elements. Example 2.5 in Seismic Principles illustrates the procedure for another wall, and provides more detailed discussion of the steps and how to be careful with units.
10. Can this detail be used for a diaphragm-to-wall connection in a structure in Seismic Design Category D?
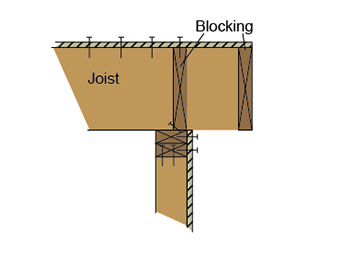
a) Yes.
b) No, because there is not an accepted mechanism for transferring in-plane wall forces.
c) No, because there is not an accepted mechanism for transferring out-of-plane wall forces.
b) No, because metal connectors/straps are required at joist-to-top-plate connections.
Solution
Best answer: (c)
Explanation
The concept is simple, but the explanation is a bit lengthy. See Section 7.5 of Seismic Principles, particularly Example 7.8.
